A collection of 15 test functions taken from the mathematical literature on Global Optimization which can be used to validate the performance of optimization algorithms.
Ackley No.1 function

This is a multimodal minimization problem defined as follows: \begin{equation*} f(\textbf{x}) = -a e^{-b\sqrt(\frac{1}{D} \sum_{i=1}^{D} x_i^2)} - e^{\frac{1}{D}cos(2\pi c x_i)} + 20 + e \end{equation*} with $x_{i} \in [-35, 35]$ and recommended values $a = 20, b = 0.2, c = 1.0$.
The global optimum is $f(0, 0) = 0$.
Beale function

This is a multimodal minimization problem defined as follows: \begin{equation*} f(x_1, x_2) = (x_1 x_2 - x_1 + 1.5)^2 + (x_1 x_2^2 - x_1 + 2.25)^2 + (x_1 x_2^3 - x_1 + 2.625)^2 \end{equation*} with $x_1, x_2 \in [-5, 5]$ and global optimum $f(3.0, 0.5) = 0$.
Booth function
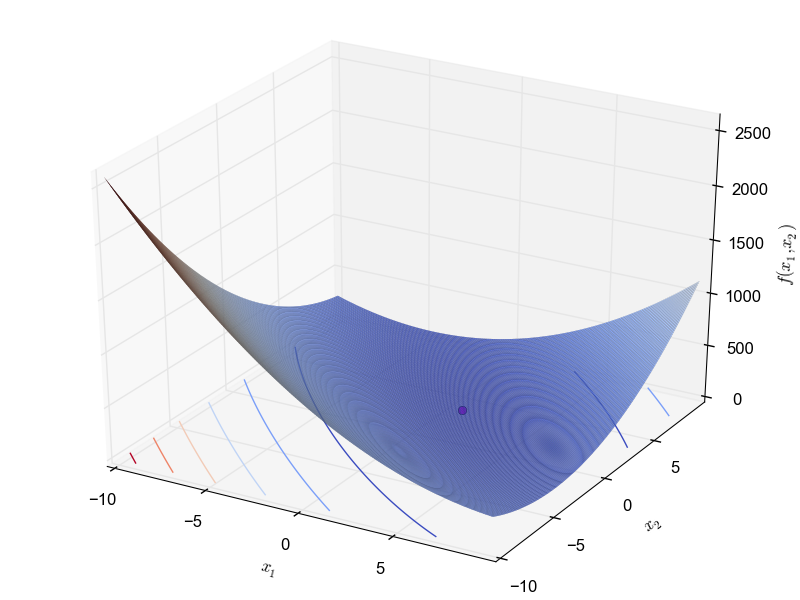
This is a unimodal minimization problem defined as follows: \begin{equation*} f(x_1, x_2) = (x_1 + 2x_2 - 7)^2 + (2x_1 + x_2 - 5)^2 \end{equation*} with $x_1, x_2 \in [-10, -10]$ and global optimum $f(1.0, 3.0) = 0$.
Bukin No.6 function
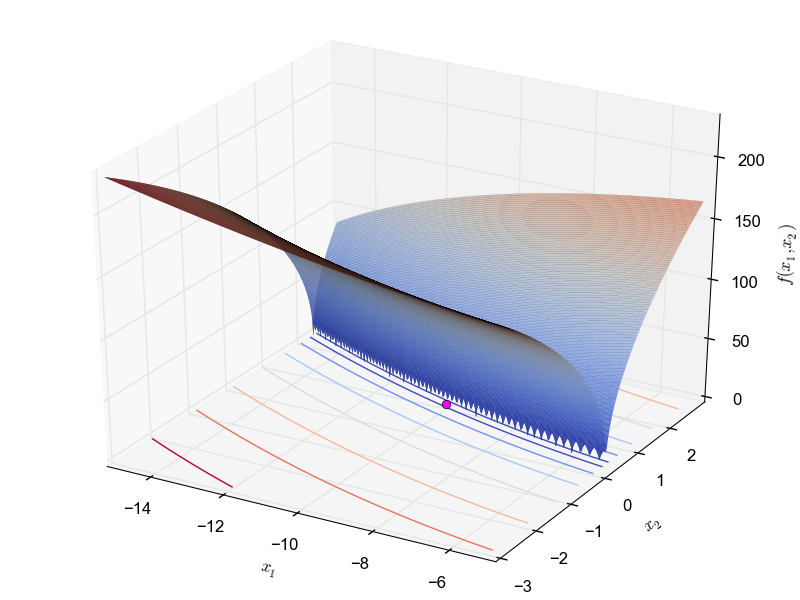
This is a multimodal minimization problem defined as follows: \begin{equation*} f(x_1, x_2) = 100 \sqrt{x_2 - 0.01x_1^2} + 0.01 |x_1 + 10| \end{equation*} with $x_1 \in [-15, -5]$ and $x_2 \in [-3, 3]$ and global optimum $f(-10.0, 1.0) = 0$.
Himmelblau function
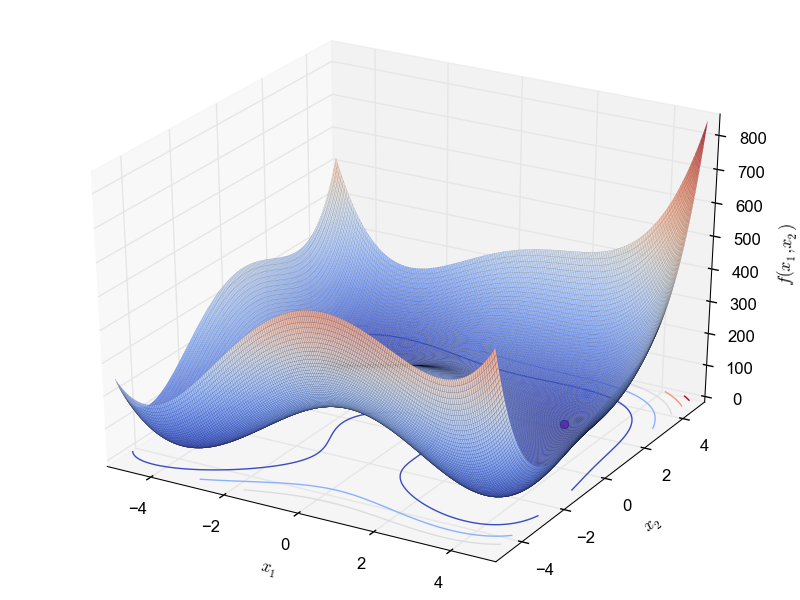
This is a multimodal minimization problem defined as follows: \begin{equation*} f(x_1, x_2) = (x_1^2 + x_2 - 11)^2 + (x_1 + x_2^2 - 7)^2 \end{equation*} with $x_1, x_2 \in [-5, 5]$ and global optimum $f(3.0, 2.0) = 0$.
Goldstein-Price function
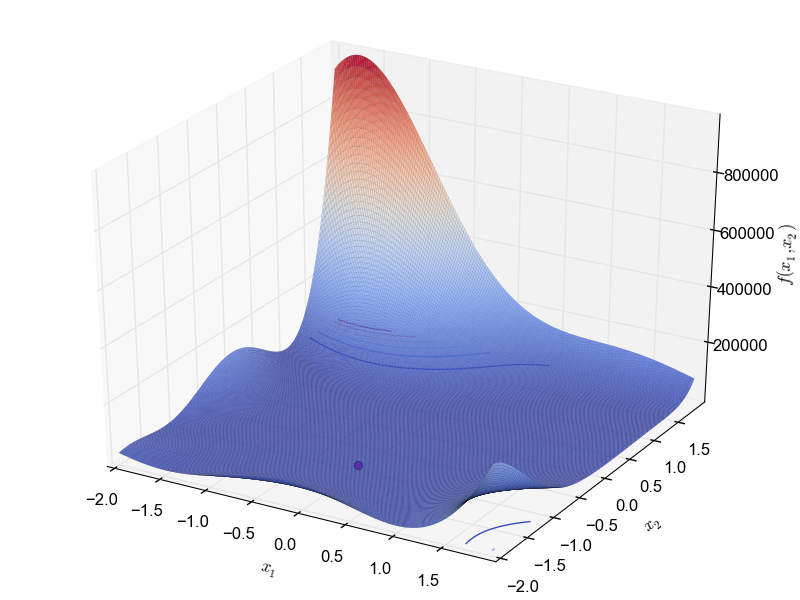
This is a multimodal minimization problem defined as follows: \begin{equation*} f(x_1, x_2) = [1 + (x_1 + x_2 + 1)^2 (19 - 14x_1 - 3x_1^2 - 14x_2 + 6x_1x_2 + 3x_2^2)] \\ [30 + (2x_1 - 3x_2)^2 (18 - 32x_1 + 12x_1^2 + 48x_2 - 36x_1x_2 + 27x_2^2)] \end{equation*} with $x_1, x_2 \in [-2, 2]$ and global optimum $f(0.0, -1.0) = 3.0$.
Levi No.13 function
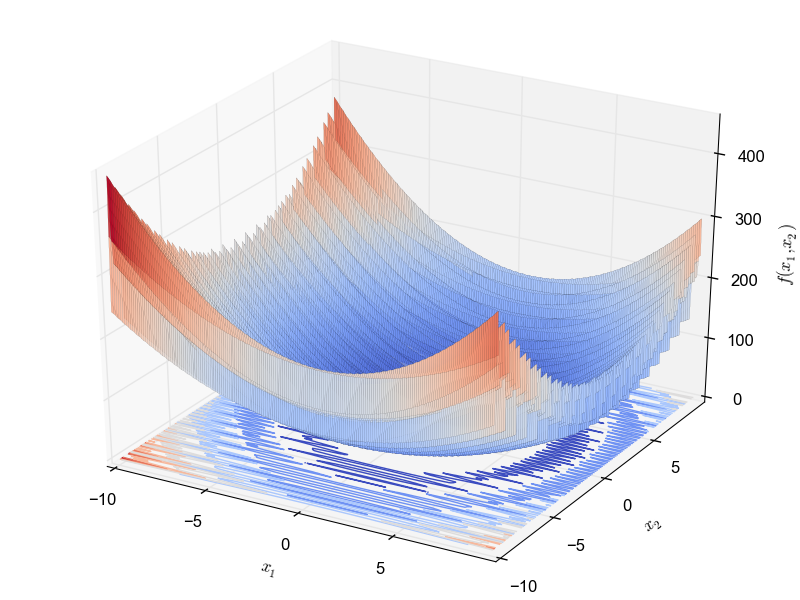
This is a multimodal minimization problem defined as follows: \begin{equation*} f(x_1, x_2) = sin(3\pi x_1)^2 + (x_1 - 1)^2 (1 + sin(3 \pi x_2)^2) + (x_2 - 1)^2 (1 + sin(2 \pi x_2)^2) \end{equation*} with $x_1, x_2 \in [-10, 10]$ and global optimum $f(1.0, 1.0) = 0.0$.
Matyas function
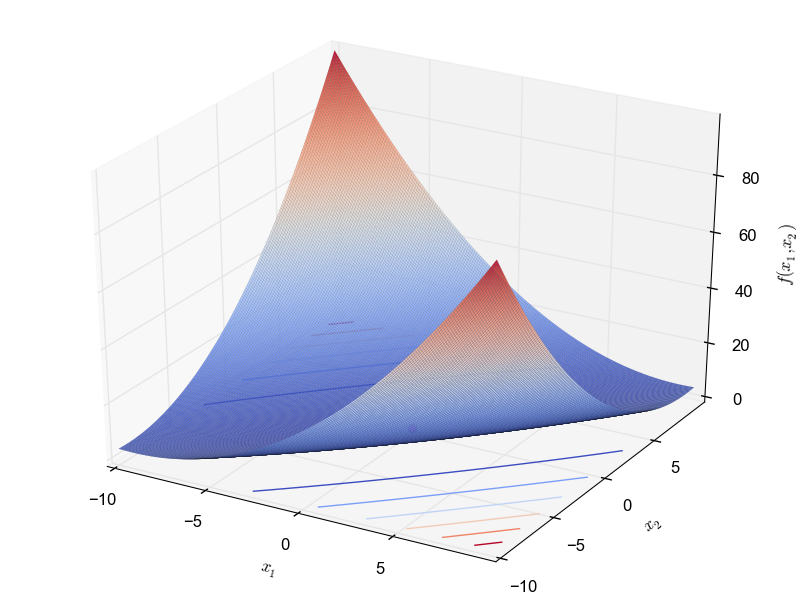
This is a multimodal minimization problem defined as follows: \begin{equation*} f(x_1, x_2) = 0.26(x_1^2 + x_2^2) - 0.48 x_1 x_2 \end{equation*} with $x_1, x_2 \in [-10, 10]$ and global optimum $f(0.0, 0.0) = 0.0$
McCormick function
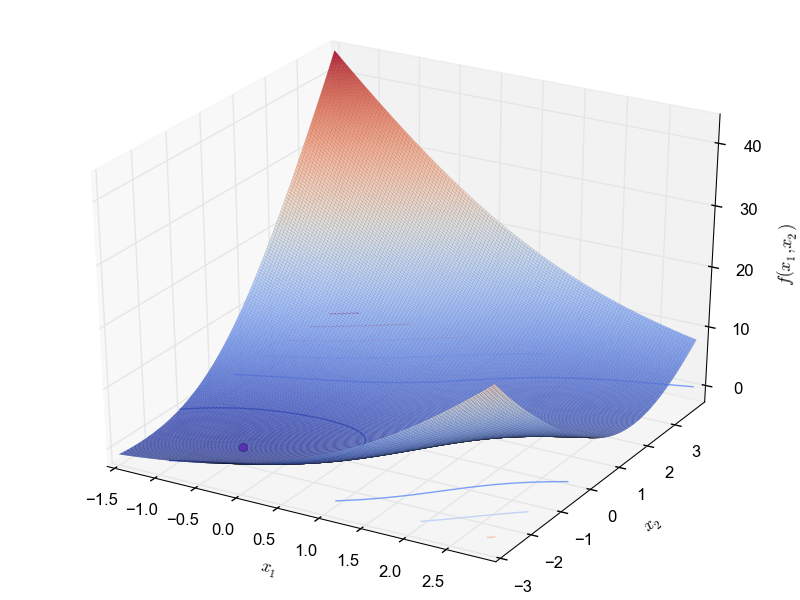
This is a multimodal minimization problem defined as follows: \begin{equation*} f(x_1, x_2) = - x_1 + 2x_2 + (x_1 - x_2)^2 + sin(x_1 + x_2) + 1 \end{equation*} with $x_1 \in [-1.5, 4.0]$ and $x_2 \in [-3.0, 4.0]$ and global optimum $f(0.0, 0.0) = 0.0$.
Rastrigin function
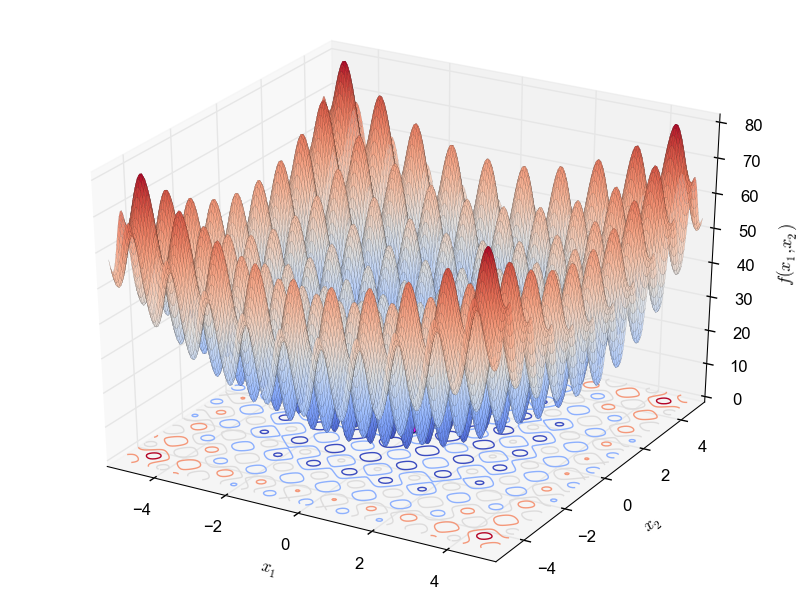
This is a highly multimodal minimization problem defined as follows: \begin{equation*} f(\textbf{x}) = 10D + \sum_{i=1}^{D}[(x_i^2 - 10cos(2\pi x_i)^2] \end{equation*} with $x_i \in [-5.12, 5.12]$ and global optimum $f(0.0,.., 0.0) = 0$
Rosenbrock function
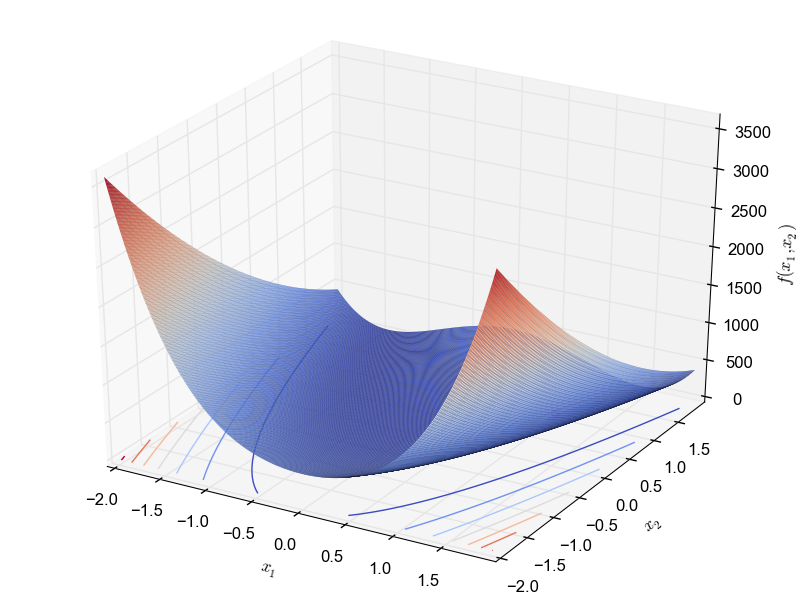
This is a multimodal minimization problem defined as follows:
\begin{equation*} f(x_1, x_2) = \sum_{i=1}^{n-1}[100(x_i^2 - x_{i+1})^2 + (x_{i} - 1)^2] \end{equation*} with $x_i \in [-2, -2]$ The best known global optimum is: $f(1.0,.., 1.0) = 0$.
Schaffer No.2 function
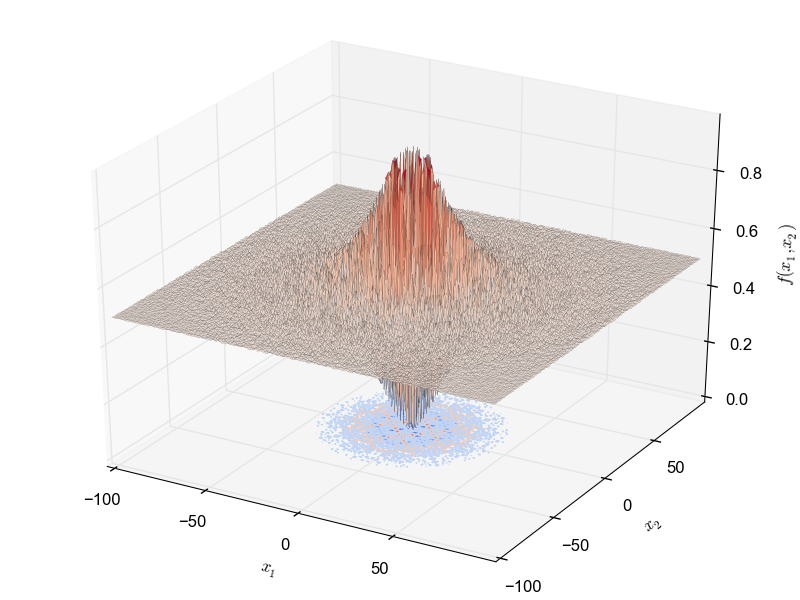
This is a unimodal minimization problem defined as follows:
\begin{equation*} f(x_1, x_2) = 0.5 + \frac{sin^2 (x_1^2 + x_2^2) - 0.5}{1 + 0.001(x_1^2 + x_2^2)^2} \end{equation*} with $x_1, x_2 \in [-100, 100]$ and global optimum $f(0.0, 0.0) = 0.0$.
Schaffer No.4 function
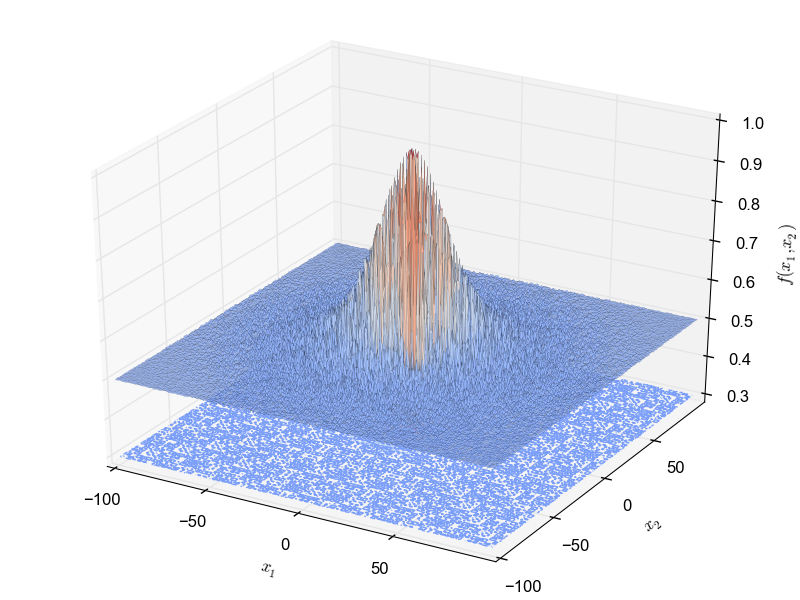
This is a unimodal minimization problem defined as follows:
\begin{equation*} f(x_1, x_2) = 0.5 + \frac{cos^2\big(sin(x_1^2 - x_2^2)\big) - 0.5}{ 1 + 0.001(x_1^2 + x_2^2)^2} \end{equation*} with $x_1, x_2 \in [-100, 100]$ and global optimum $f(0.0, 1.253115) = 0.292579$.
Styblinski-Tang function

This is a multimodal minimization problem defined as follows:
\begin{equation*} f(x_1, x_2) = \frac{1}{2}\sum_{i=1}^{D} (x_i^4 - 16x_i^2 + x_i) \end{equation*} with $x_1, x_2 \in [-5, 5]$ and global optimum $f(-2.903534, -2.903534) = -78.332$.
Zettl function
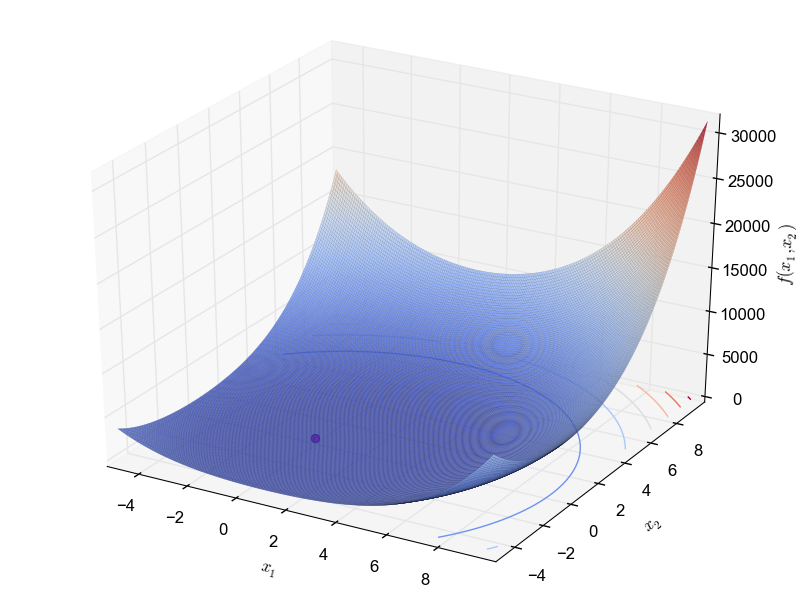
This is a unimodal minimization problem defined as follows:
\begin{equation*} f(x_1, x_2) = 0.25 x_1 + (x_1^2 - 2 x_1 + x_2^2)^2 \end{equation*} with $x_1, x_2 \in [-5, 10]$ and global optimum $f(-0.029896, 0.0) = -0.003791$.
References
- Jamil M. and Yang X.S. (2013). A literature survey of benchmark functions for global optimization problems, International Journal of Mathematical Modeling and Numerical Optimization, 4(2), 150 - 194.
- Floudas C.A. and Pardalos P.M. (1987). A Collection of Test Problems for Constrained Global Optimization Algorithms, Springer.
- http://en.wikipedia.org/wiki/Test_functions_for_optimization.
